k-Nearest Neighbors Regression Example

The example below illustrates the use of Analytic Solver Data Science’s k-Nearest Neighbors Regression method using the Boston_Housing.xlsx dataset.

Input

Click Help – Example Models on the Data Science ribbon to open the Examples Overview dialog.  Select Forecasting/Data Science Examples, then click the Boston Housing link to open Boston_Housing.xlsx.  This dataset contains 14 variables, the description of each is given in the Description worksheet included within the example workbook.  The dependent variable MEDV is the median value of a dwelling.  The objective of this example is to predict the value of this variable.  A portion of the dataset is shown below.   

Note:  All supervised algorithms include a new Simulation tab.  This tab uses the functionality from the Generate Data feature to generate synthetic data based on the training partition, and uses the fitted model to produce predictions for the synthetic data.  The resulting report, KNNP_Simulation, will contain the synthetic data, the predicted values and the Excel-calculated Expression column, if present.  Since this new functionality does not support categorical variables, the CHAS variable will not be included in the k-Nearest Neighbors prediction model.  The last variable, CAT. MEDV, is a discrete classification of the MEDV variable and will also not be used in this example.

Partition the data into training and validation sets using the Standard Data Partition defaults with percentages of 60% of the data randomly allocated to the Training Set and 40% of the data randomly allocated to the Validation Set.  

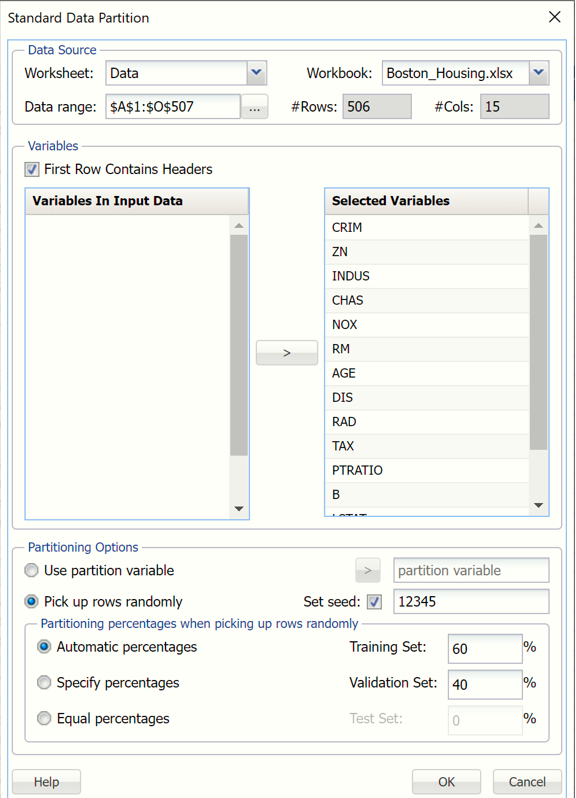
• Note:  If using Analytic Solver Desktop, the STDPartition worksheet is inserted into the Model tab of the Analytic Solver task pane under Transformations -- Data Partition and the data used in the partition will appear under Data, as shown in the screenshot below.

Click Predict – k-Nearest Neighbors to open the k-Nearest Neighbors regression dialog. 

Select MEDV as the Output Variable, and the remaining variables (except CAT. MEDV, CHAS, and Record ID) as Selected Variables.

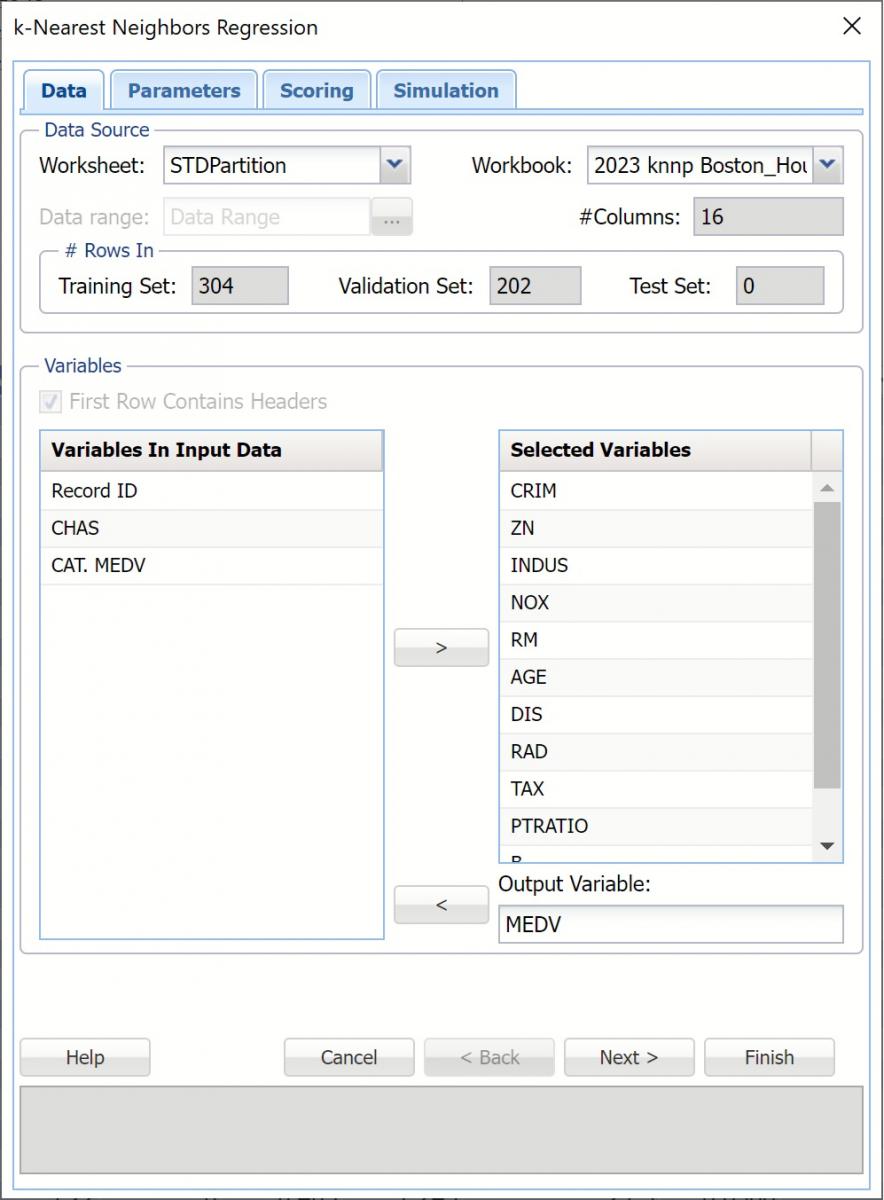
Click Next to advance to the Parameters tab.

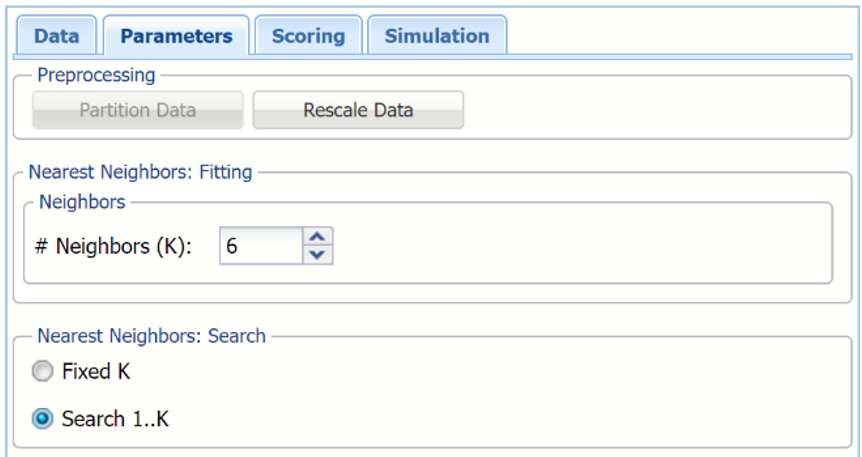
Analytic Solver Data Science includes the ability to partition and rescale a dataset from within a classification or regression method by selecting Partition Data and/or Rescale Data on the Parameters tab.  If both or either of these options are selected, Analytic Solver Data Science will partition and/or rescale your dataset (according to the partition and rescaling options you set) immediately before running the regression method.  If partitioning has already occurred on the dataset, the Partition Data button will be disabled. 

Enter 6 for # Neighbors (K).  (This number is based on standard practice from the literature.)  This is the parameter k in the k-Nearest Neighbor algorithm. 

If the number of observations (rows) is less than 50 then the value of k should be between 1 and the total number of observations (rows). If the number of rows is greater than 50, then the value of k should be between 1 and 50.  Note that if k is chosen as the total number of observations in the training set, then for any new observation, all the observations in the training set become nearest neighbors.  The default value for this option is 1.  

Select Search 1..K under Nearest Neighbors Search.  When this option is selected, Analytic Solver Data Science will display the output for the best k between 1 and the value entered for # Neighbors.  If Fixed K is selected, the output will be displayed for the specified value of k.

Click Next to advance to the Scoring tab. 

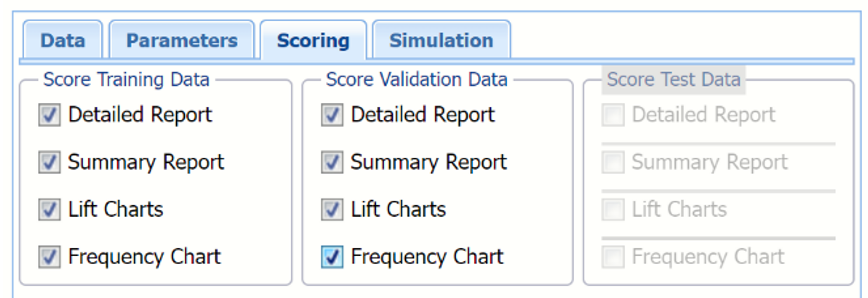
Select all four options for Score Training/Validation data. 

When Detailed report is selected, Analytic Solver Data Science will create a detailed report of the k-Nearest Neighbors output. 

When Summary report is selected, Analytic Solver Data Science will create a report summarizing the k-Nearest Neighbors output.

When Lift Charts is selected, Analytic Solver Data Science will include Lift Chart and RROC Curve  plots in the output.

When Frequency Chart is selected, a frequency chart will be displayed when the KNNP_TrainingScore and KNNP_ValidationScore worksheets are selected.  This chart will display an interactive application similar to the Analyze Data feature, explained in detail in the Analyze Data chapter that appears earlier in this guide.  This chart will include frequency distributions of the actual and predicted responses individually, or side-by-side, depending on the user’s preference, as well as basic and advanced statistics for variables, percentiles, six sigma indices. 

Since we did not create a test partition, the options for Score test data are disabled.  See the chapter “Data Science Partitioning” for information on how to create a test partition. 

See the Scoring New Data chapter within the Analytic Solver Data Science User Guide for more information on Score New Data in options. 

Click Next to advance to the Simulation tab. 

Select Simulation Response Prediction to enable all options on the Simulation tab of the k-Nearest Neighbors Regression dialog. 

Simulation tab: As mentioned above, all supervised algorithms include a new Simulation tab.  This tab uses the functionality from the Generate Data feature to generate synthetic data based on the training partition, and uses the fitted model to produce predictions for the synthetic data.  The resulting report, KNNP_Simulation, will contain the synthetic data, the predicted values and the Excel-calculated Expression column, if present.  In addition, frequency charts containing the Predicted, Training, and Expression (if present) sources or a combination of any pair may be viewed, if the charts are of the same type. 

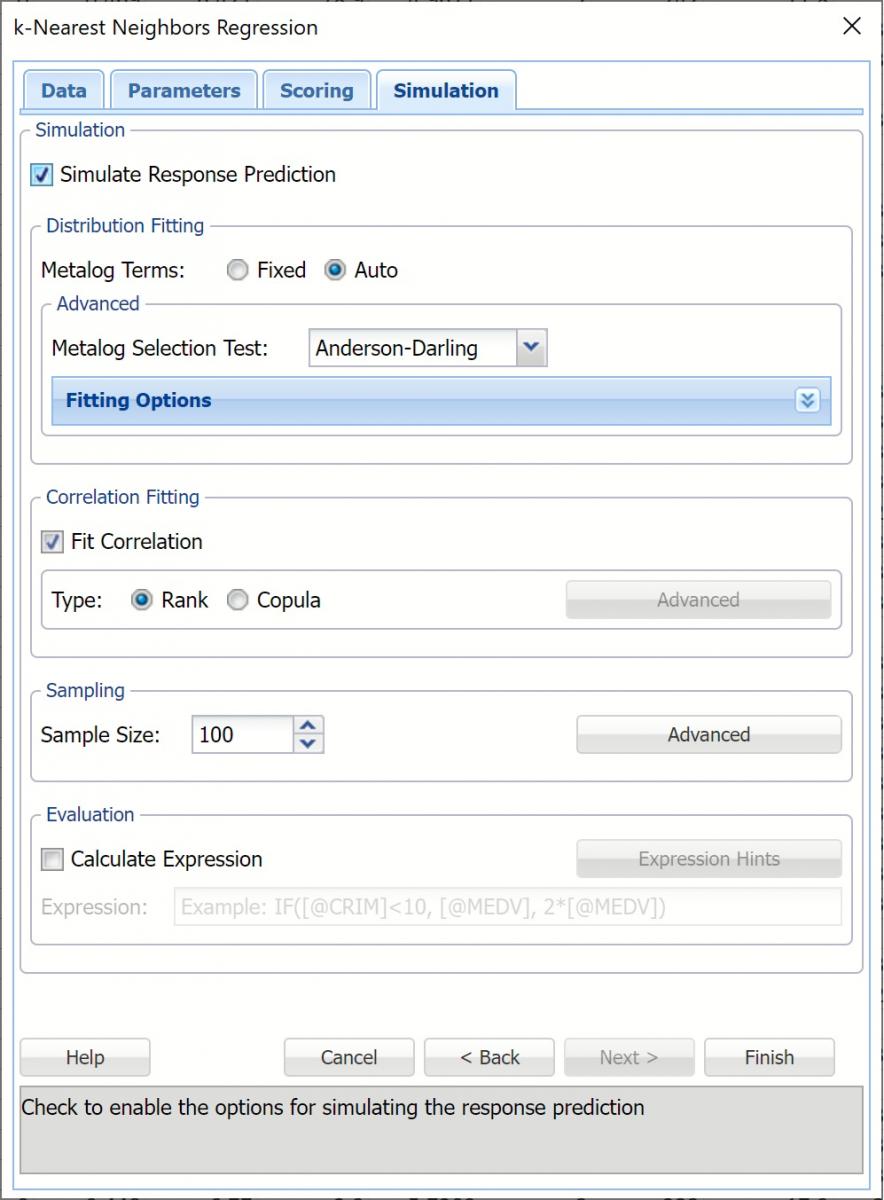
Evaluation:  Select Calculate Expression to amend an Expression column onto the frequency chart displayed on the KNNP_Simulation output tab.  Expression can be any valid Excel formula that references a variable and the response as [@COLUMN_NAME].  Click the Expression Hints button for more information on entering an expression.  Note that variable names are case sensitive. 

For the purposes of this example, leave all options at their defaults in the Distribution Fitting, Correlation Fitting, Sampling and Evaluation sections of the dialog. For more information on these options, see Generate Data.  

Click Finish to run k-Nearest Neighbors Prediction on the example dataset. 

Output

Output sheets containing the results of the k-Nearest Neighbors Prediction model will be inserted into your active workbook to the right of the STDPartition worksheet. 

KNNP_Output

This result worksheet includes 3 segments:  Output Navigator, Inputs and the Search Log. 

• Output Navigator:  The Output Navigator appears at the top of all result worksheets.  Use this feature to quickly navigate to all reports included in the output. 

KNNP_Output:  Output Navigator

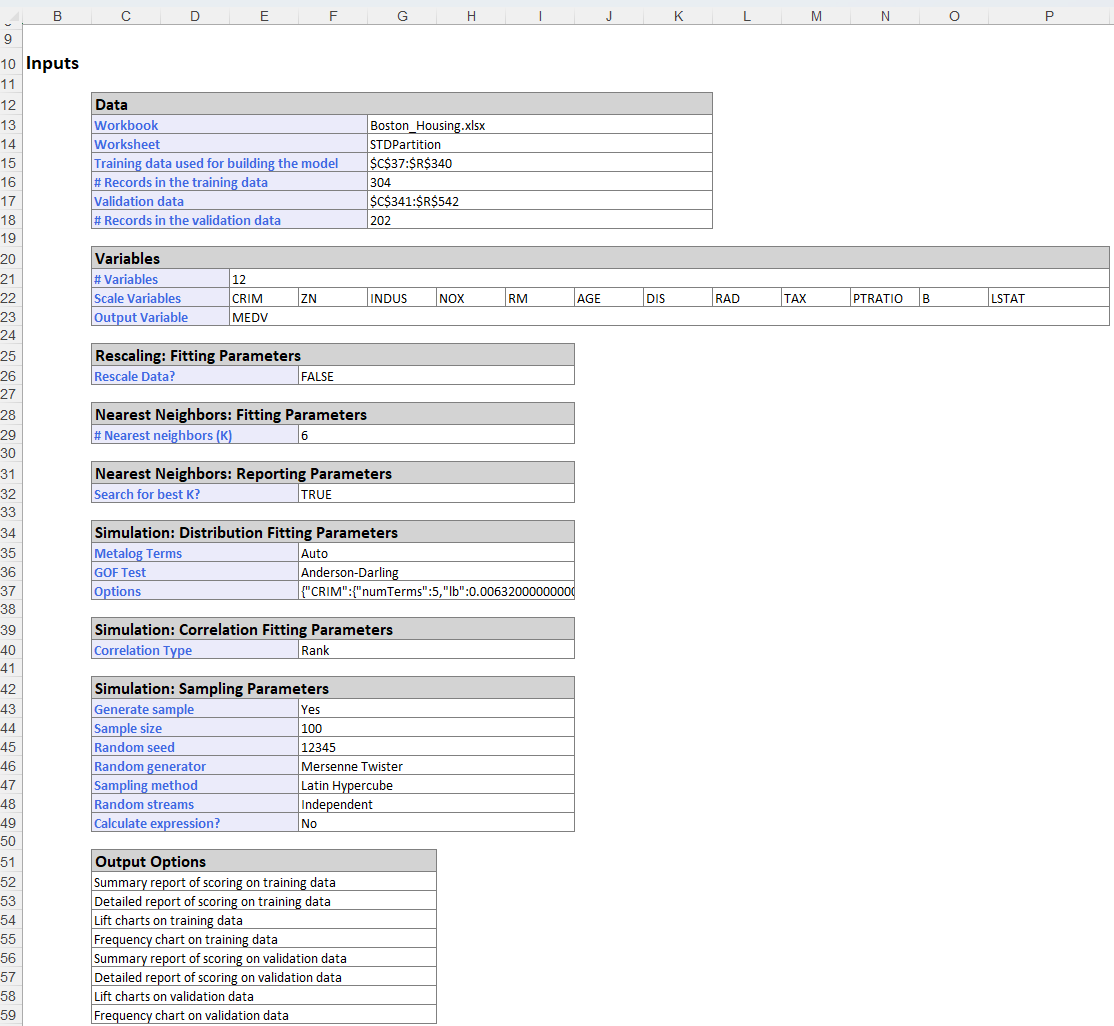
• Inputs:  Scroll down to the Inputs section to find all inputs entered or selected on all tabs of the k-Nearest Neighbors Prediction dialog.

KNNP_Output:  Inputs

• Search Log:  Scroll down KNNP_Output to the Search Log report (shown below).  As per our specifications, Analytic Solver Data Science has calculated the RMS error for all values of k and denoted the value of k with the smallest RMS Error.  The validation partition will be scored using this value of k.

 

KNNP_TrainingScore

Click the KNNP_TrainingScore tab to view the newly added Output Variable frequency chart, the Training:  Prediction Summary and the Training:  Prediction Details report.  All calculations, charts and predictions on this worksheet apply to the Training data. 

Note:  To view charts in the Cloud app, click the Charts icon on the  Ribbon, select a worksheet under Worksheet and a chart under Chart. 

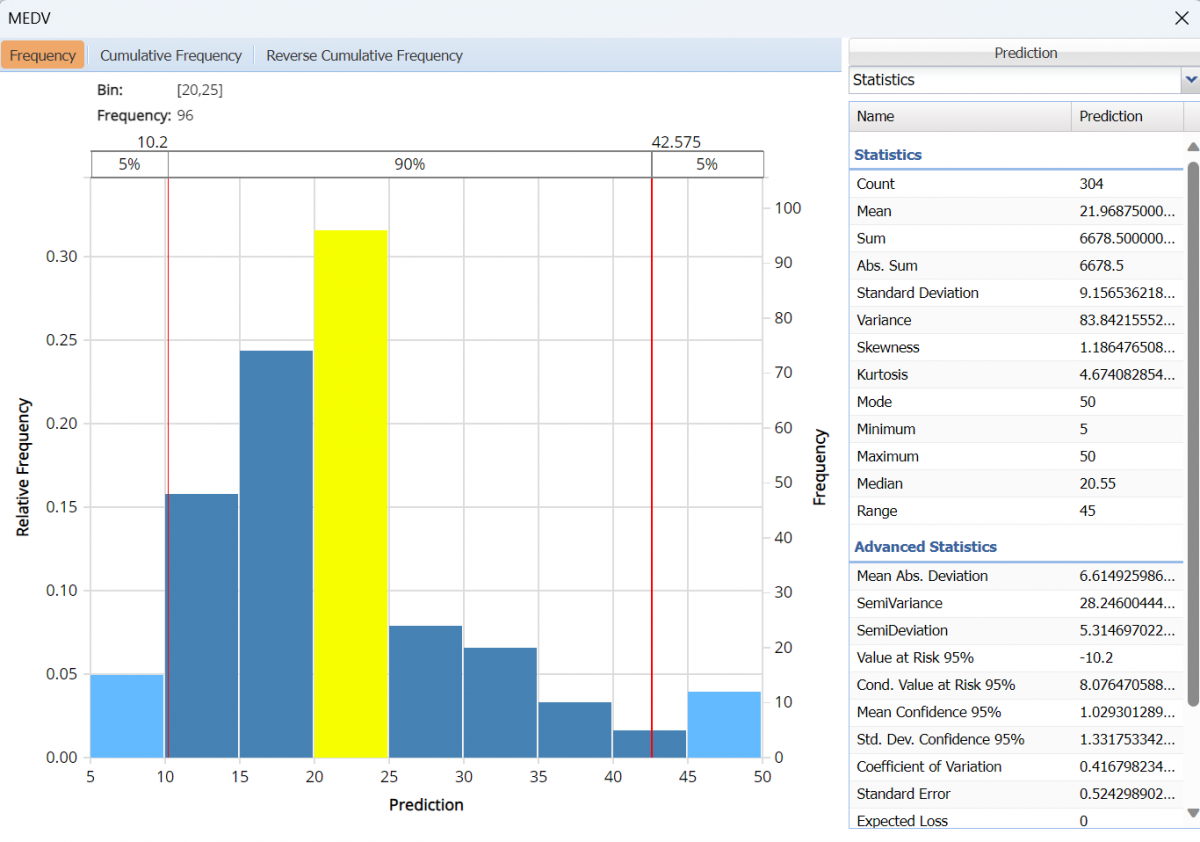
Frequency Charts:  The output variable frequency chart for the training partition opens automatically once the KNNP_TrainingScore worksheet is selected. To close this chart, click the “x” in the upper right hand corner of the chart.  To reopen, click onto another tab and then click back to the KNNP_TrainingScore tab.    To move the dialog to a new location on the screen, simply grab the title bar and drag the dialog to the desired location.  This chart displays a detailed, interactive frequency chart for the Actual variable data and the Predicted data, for the training partition. 

Predicted values for training partition, MEDV variable

To display the predicted values and the actual data at the same time, click Prediction in the upper right hand corner and select both checkboxes in the Data dialog.

Click Prediction, then select Actual to add original data to the interactive chart

Actual vs Predicted values for Training Partition, MEDV variable

Notice in the screenshot below that both the Actual and Prediction data appear in the chart together, and statistics for both data appear on the right. 

Statistics Pane

To remove either the Actual or Prediction data from the chart, click Prediction/Actual in the top right and then uncheck the data type to be removed. 

This chart behaves the same as the interactive chart in the Analyze Data feature found on the Explore menu.  Click here for more information.   

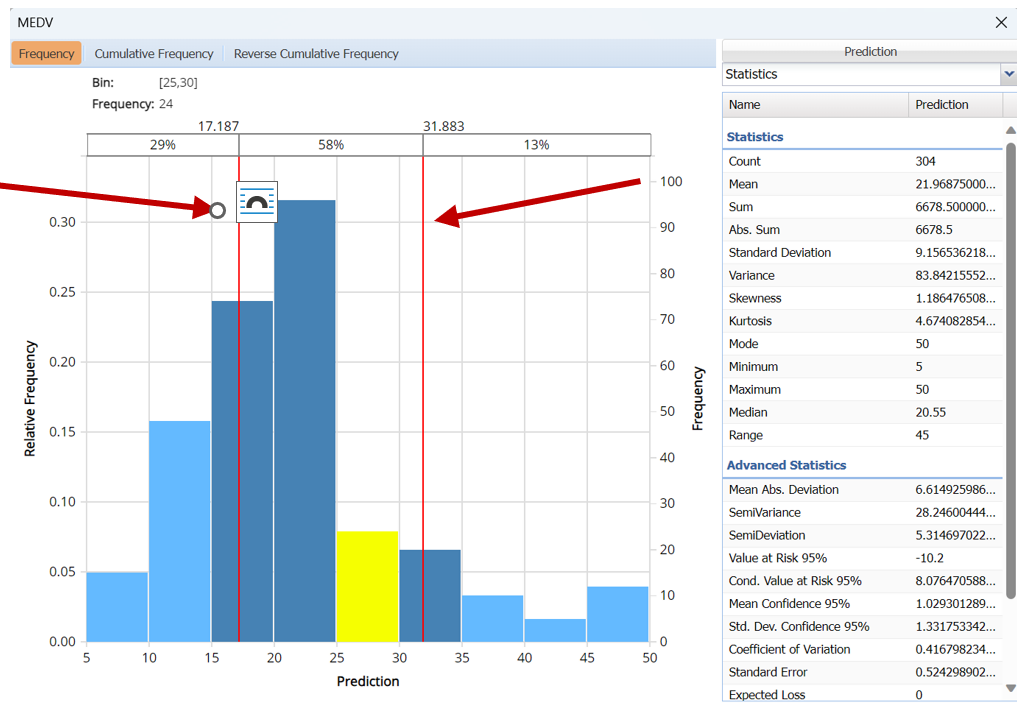
• Use the mouse to hover over any of the bars in the graph to populate the Bin and Frequency headings at the top of the chart. 
• When displaying either Original or Synthetic data (not both), red vertical lines will appear at the 5% and 95% percentile values in all three charts (Frequency, Cumulative Frequency and Reverse Cumulative Frequency) effectively displaying the 90th confidence interval. The middle percentage is the percentage of all the variable values that lie within the ‘included’ area, i.e. the darker shaded area. The two percentages on each end are the percentage of all variable values that lie outside of the ‘included’ area or the “tails”. i.e. the lighter shaded area.  Percentile values can be altered by moving either red vertical line to the left or right. 

Frequency Chart for MEDV Prediction with red percentile lines moved

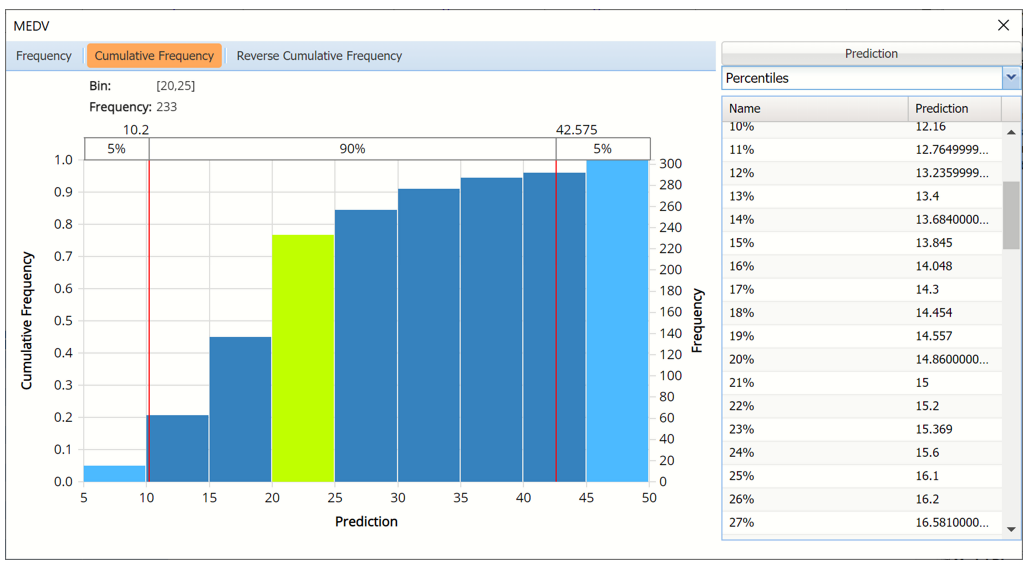
• Click Cumulative Frequency and Reverse Cumulative Frequency tabs to see the Cumulative Frequency and Reverse Cumulative Frequency charts, respectively.
• Select Percentiles from the drop down menu to view Percentile values.  

Cumulative Frequency chart with Percentiles displayed

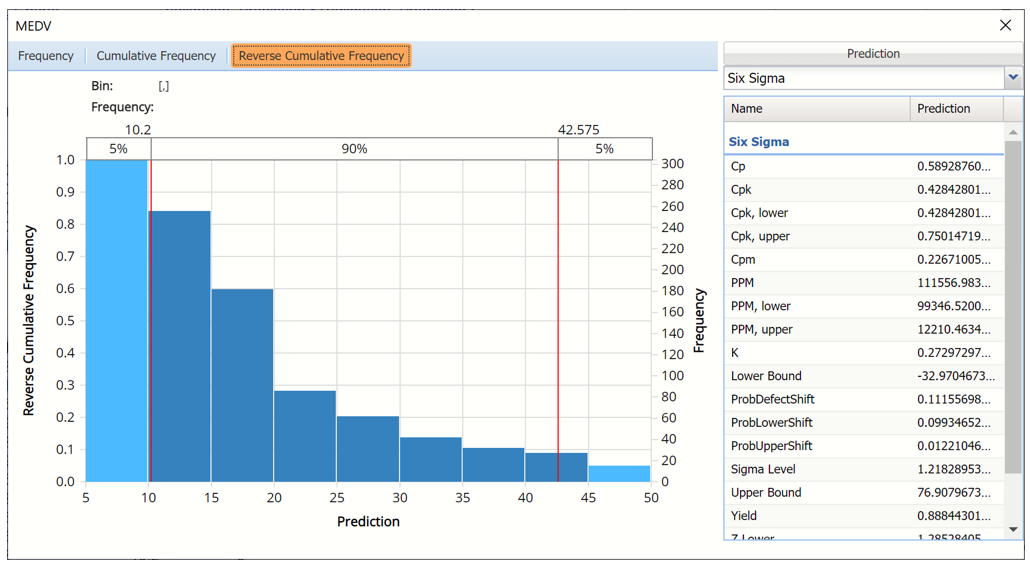
• Select Six Sigma from the drop down menu to view the Six Sigma indices.

Reverse Cumulative Frequency chart with Six Sigma indices displayed 

• Select Bin Details from the drop down menu to view Bin Details for each bin in the chart.
• Use the Chart Options view to manually select the number of bins to use in the chart, as well as to set personalization options. 

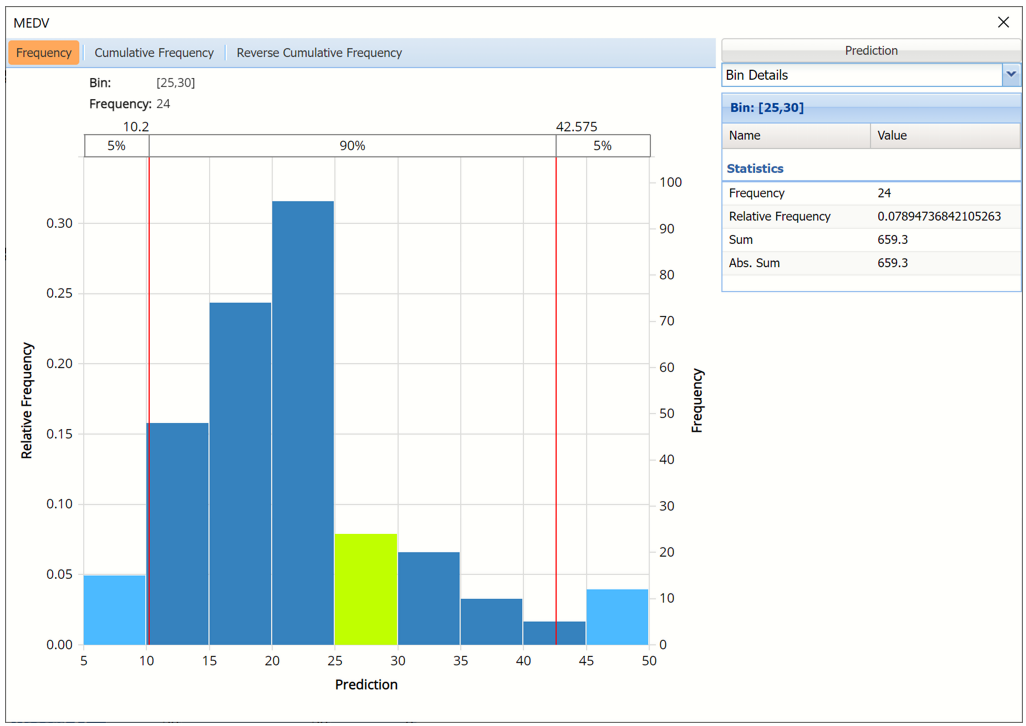
As discussed above, see Analyze Data for an in-depth discussion of this chart as well as descriptions of all statistics, percentiles, bin details and six sigma indices. 

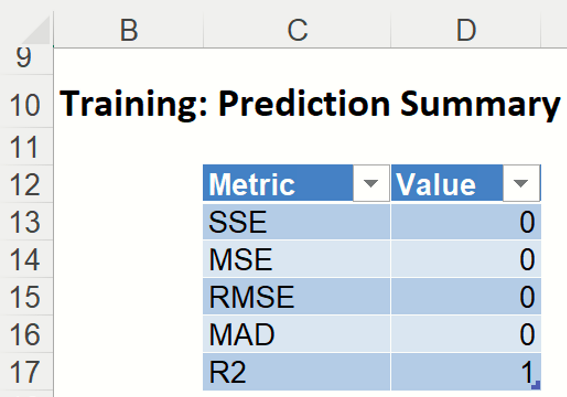
• Prediction Summary:  A key interest in a data-mining context will be the predicted and actual values for the MEDV variable along with the residual (difference) for each predicted value in the Training partition. 

The Training:  Prediction Summary report summarizes the prediction error. The first number, the total sum of squared errors, is the sum of the squared deviations (residuals) between the predicted and actual values. The second is the average of the squared residuals, the third is the square root of the average of the squared residuals and the fourth is the average deviation. All these values are calculated for the best k, i.e. k=6. Note that the algorithm perfectly predicted the correct median selling price for each census tract in the training partition. 

Training Prediction Summary

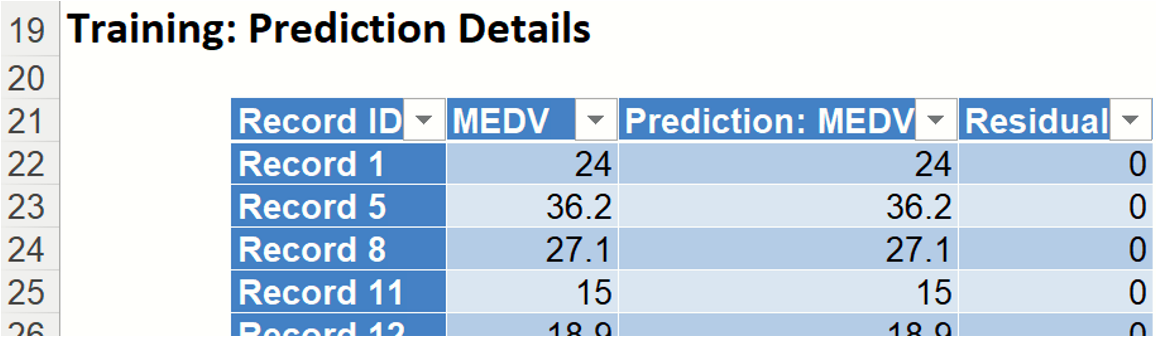
• Prediction Details displays the predicted value, the actual value and the difference between them (the residuals), for each record. 

KNNP_ValidationScore

A key interest in a data-mining context will be the predicted and actual values for the MEDV variable along with the residual (difference) for each predicted value in the Validation partition. 

KNNP_ValidationScore displays the newly added Output Variable frequency chart, the Validation:  Prediction Summary and the Validation:  Prediction Details report.  All calculations, charts and predictions on the KNNP_ValidationScore output sheet apply to the Validation partition.

• Frequency Charts:  The output variable frequency chart for the validation partition opens automatically once the KNNP_ValidationScore worksheet is selected. This chart displays a detailed, interactive frequency chart for the Actual variable data and the Predicted data, for the validation partition.  For more information on this chart, see the KNNP_TrainingScore explanation above. 

Validation Partition Frequency Chart

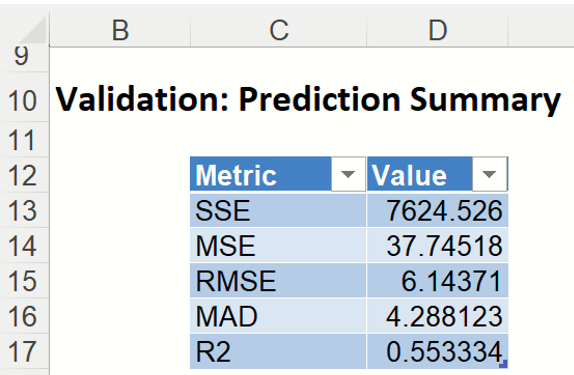
• Prediction Summary:  In the Prediction Summary report, Analytic Solver Data Science displays the total sum of squared errors summaries for the Validation partition. 

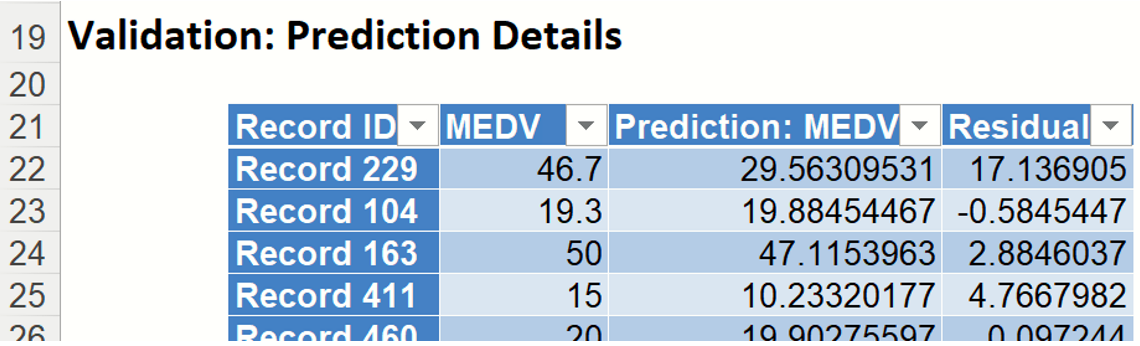
• Prediction Details:  Scroll down to the Validation:  Prediction Details report to find the Prediction value for the MEDV variable for each record, as well as the Residual value, in the Validation partition.

KNNP_TrainingLiftChart and KNNP_ValidationLiftChart

Lift charts and RROC Curves (on the KNNP_TrainingLiftChart and KNNP_ValidationLiftChart tabs, respectively) are visual aids for measuring model performance. Lift Charts consist of a lift curve and a baseline. The greater the area between the lift curve and the baseline, the better the model.  RROC (regression receiver operating characteristic) curves plot the performance of regressors by graphing over-estimations (or predicted values that are too high)  versus underestimations (or predicted values that are too low.)  The closer the curve is to the top left corner of the graph (in other words, the smaller the area above the curve), the better the performance of the model. 

After the model is built using the training data set, the model is used to score on the training data set and the validation data set (if one exists). Then the data set(s) are sorted in descending order using the predicted output variable value.  After sorting, the actual outcome values of the output variable are cumulated and the lift curve is drawn as the number of cases versus the cumulated value. The baseline (red line connecting the origin to the end point of the blue line) is drawn as the number of cases versus the average of actual output variable values multiplied by the number of cases.

The decilewise lift curve is drawn as the decile number versus the cumulative actual output variable value divided by the decile's mean output variable value.  The bars in this chart indicate the factor by which the kNNP model outperforms a random assignment, one decile at a time.  Refer to the validation graph below.  In the first decile in both the training and validation datasets, taking the most expensive predicted housing prices in the dataset, the predictive performance of the model is about 1.8 times better as simply assigning a random predicted value.

Note:  To view these charts in the Cloud app, click the Charts icon on the  Ribbon, select KNNP_TrainingLiftChart or KNNP_ValidationLiftChart for Worksheet and Decile Chart, RROC Chart or Gain Chart for Chart.

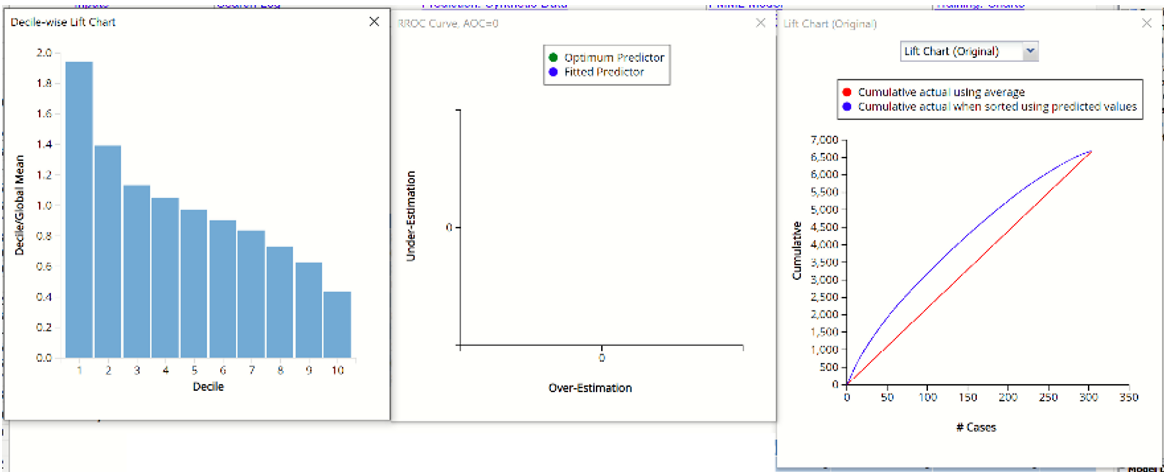
Decile-Wise Lift Chart, RROC Curve and Lift Chart from Training Partition

Decile-Wise Lift Chart, RROC Curve and Lift Chart from Validation Partition

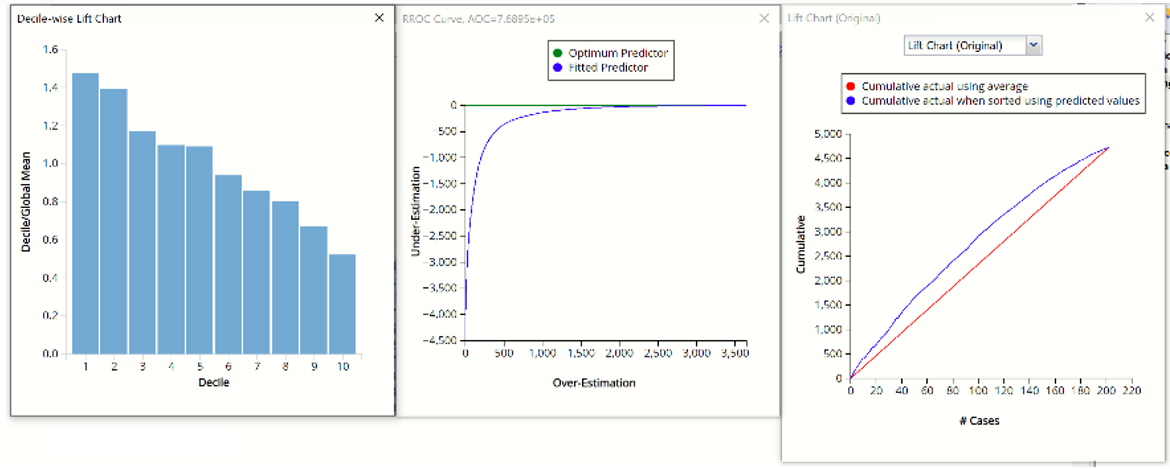
In an RROC curve, we can compare the performance of a regressor with that of a random guess (red line) for which under estimations are equal to over-estimations shifted to the minimum under estimate.  Anything to the left of this line signifies a better prediction and anything to the right signifies a worse prediction.  The best possible prediction performance would be denoted by a point at the top left of the graph at the intersection of the x and y axis.  Area Over the Curve (AOC) is the space in the graph that appears above the RROC curve and is calculated using the formula: sigma2 * n2/2 where n is the number of records   The smaller the AOC, the better the performance of the model. The RROC Curve for the Training Partition is blank.  This is because the KNN algorithm perfectly predicted the selling price in the training partition.   

In V2017, two new charts were introduced:  a new Lift Chart and the Gain Chart.  To display these new charts, click the down arrow next to Lift Chart (Original), in the Original Lift Chart, then select the desired chart. 

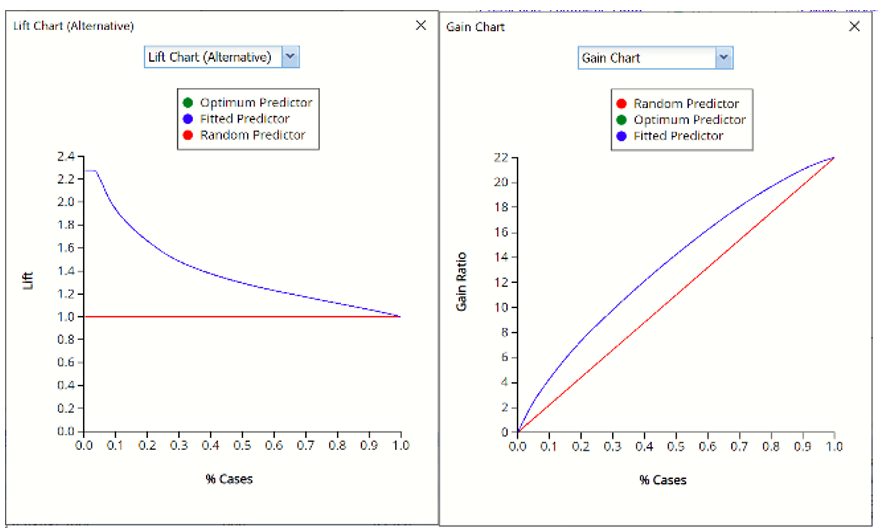
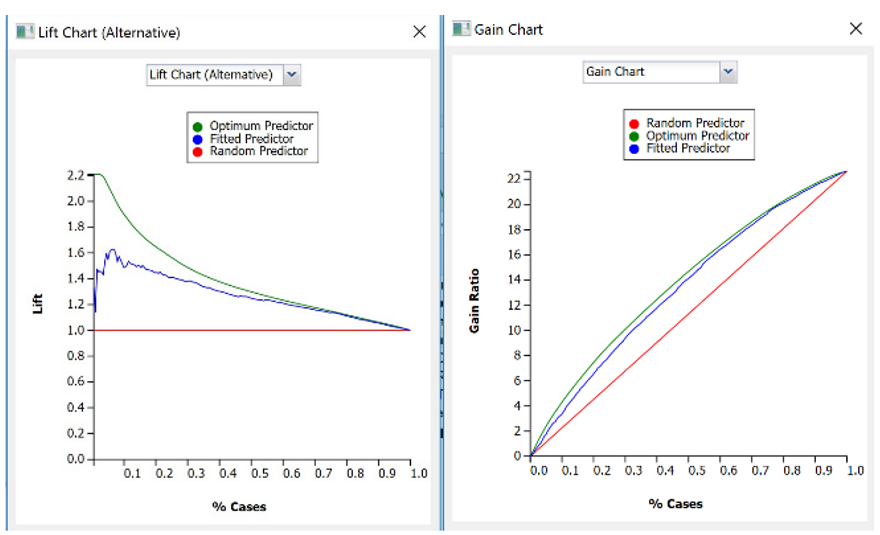
Select Lift Chart (Alternative) to display Analytic Solver Data Science's new Lift Chart.  Each of these charts consists of an Optimum Predictor curve, a Fitted Predictor curve, and a Random Predictor curve.  The Optimum Predictor curve plots a hypothetical model that would provide a perfect fit to the data.  The Fitted Predictor curve plots the fitted model and the Random Predictor curve plots the results from using no model or by using a random guess. 

The Alternative Lift Chart plots Lift against % Cases.  The Gain Chart plots the Gain Ratio against % Cases. 

Lift Chart (Alternative) and Gain Chart for Training Partition

Lift Chart (Alternative) and Gain Chart for Validation Partition

  

KNNP_Simulation

As discussed above, Analytic Solver Data Science generates a new output worksheet, KNNP_Simulation, when Simulate Response Prediction is selected on the Simulation tab of the k-Nearest Neighbors dialog. 

This report contains the synthetic data, the predicted values for the training partition (using the fitted model) and the Excel – calculated Expression column, if populated in the dialog.  Users can switch between the Predicted, Training, and Expression sources or a combination of two, as long as they are of the same type. 

Synthetic Data

The data contained in the Synthetic Data report is syntethic data, generated using the Generate Data feature.    

The chart that is displayed once this tab is selected, contains frequency information pertaining to the output variable in the training data, the synthetic data and the expression, if it exists.  (Recall that no expression was entered in this example.)

Frequency Chart for Prediction (Simulation) data

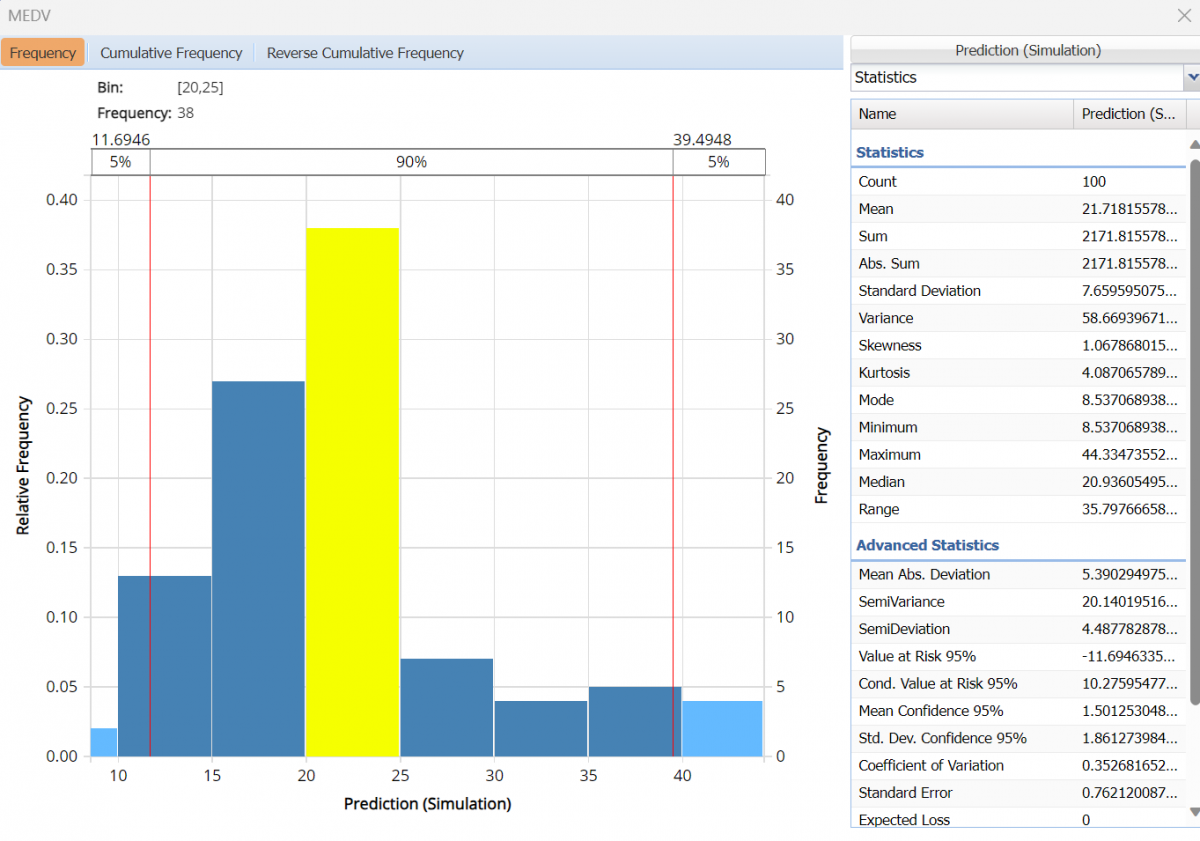
To change the data view, click the Prediction (Simulation) button.  Select Prediction (Training) and Prediction (Simulation) to add the training data to the chart.

Data Dialog

In the chart below, the darker blue bars represent the predictions for the synthetic data while the lighter blue bars represent the predictions for the training data. 

Prediction (Simulation) and Prediction (Training) Frequency chart for MEDV variable

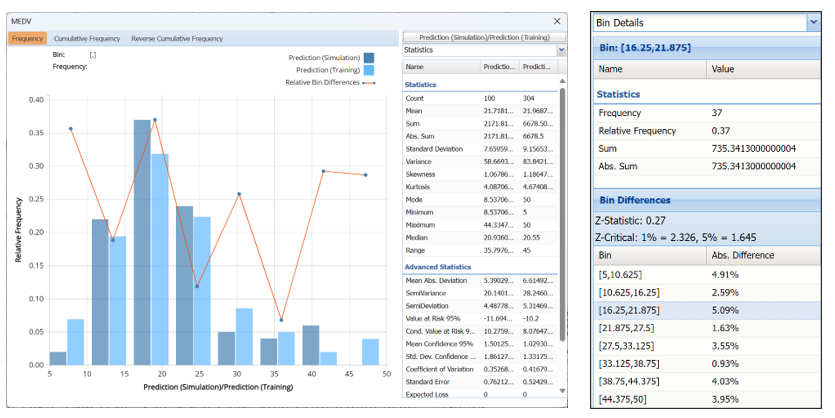
The Relative Bin Differences curve charts the absolute differences between the data in each bin.  Click the down arrow next to Statistics to view the Bin Details pane to display the calculations.

Statistics on the right of the chart dialog are discussed earlier in this help topic.  For more information on the generated synthetic data, see the Generate Data. 

KNNP_Stored

For information on Stored Model Sheets, in this example KNNP_Stored, please refer to the “Scoring New Data” chapter that apperas later in this guide.