| Logistic regression is a variation of ordinary regression that is used when the dependent (response) variable is dichotomous (i. e., takes two values). The dichotomous variable represents the occurrence or non-occurrence of some outcome event, usually coded as 0 or 1, and the independent (input) variables are continuous, categorical, or both (i.e., in a medical study, the patient survives or does not survive).
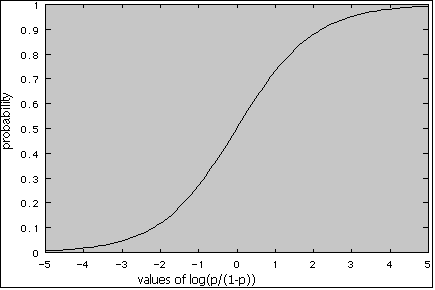
Unlike ordinary linear regression, logistic regression does not assume that the relationship between the independent and dependent variables are linear. Nor does it assume that the dependent variable or the error terms are distributed normally. In logistic regression, a binary logistic model is used to estimate the probability of a binary response based on one or more predictor or independent variables. The binary logistic model is displayed as in the following  where, p is the probability that Y=1 and X1, X2,.. .,Xk are the independent variables (predictors). b0 , b1, b2, .... bk are known as the regression coefficients, which are estimated from the data. Logistic regression estimates the probability of a certain event occurring. Logistic regression thus forms a predictor variable (log (p/(1-p)) that is a linear combination of the explanatory variables. The values of this predictor variable are then transformed into probabilities by a logistic function. Such a function has the shape of an S. The values of the predictor variable are displayed on the horizontal axis, and the probabilities are on the vertical axis.
|